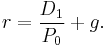Dividend discount model
The dividend discount model (DDM) is a way of valuing a company based on the theory that a stock is worth the discounted sum of all of its future dividend payments.[1] In other words, it is used to value stocks based on the net present value of the future dividends. The equation most always used is called the Gordon growth model. It is named after Myron J. Gordon, who originally published it in 1959.[2].
The variables are:  is the current stock price.
is the current stock price.  is the constant growth rate in perpetuity expected for the dividends.
is the constant growth rate in perpetuity expected for the dividends.  is the constant cost of equity for that company.
is the constant cost of equity for that company. 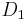 is the value of the next year's dividends. There is no reason to use a calculation of next year's dividend using the current dividend and the growth rate, when management commonly disclose the future year's dividend and websites post it.
is the value of the next year's dividends. There is no reason to use a calculation of next year's dividend using the current dividend and the growth rate, when management commonly disclose the future year's dividend and websites post it.
Contents |
Derivation of equation
The model sums the infinite series which gives the current price P.
Income plus capital gains equals total return
The equation can also be understood to generate the value of a stock such that the sum of its dividend yield (income) plus its growth (capital gains) equals the investor's required total return. Consider the dividend growth rate as a proxy for the growth of earnings and by extension the stock price and capital gains. Consider the company's cost of equity capital as a proxy for the investor's required total return.
Growth cannot exceed cost of equity
From the first equation, one might notice that 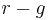 cannot be negative. When growth is expected to exceed the cost of equity in the short run, then usually a two stage DDM is used:
cannot be negative. When growth is expected to exceed the cost of equity in the short run, then usually a two stage DDM is used:
Therefore,
where  denotes the short-run expected growth rate,
denotes the short-run expected growth rate, 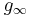 denotes the long-run growth rate, and
denotes the long-run growth rate, and  is the period (number of years), over which the short-run growth rate is applied.
is the period (number of years), over which the short-run growth rate is applied.
Even when g is very close to r, P approaching infinity, so the model becomes meaningless.
Some properties of the model
a) When the growth g is zero the dividend is capitalized.
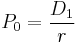 .
.
b) This equation is also used to estimate cost of capital by solving for  .
.
Problems with the model
a) The presumption of a steady and perpetual growth rate less than the cost of capital may not be reasonable.
b) If the stock does not currently pay a dividend, like many growth stocks, more general versions of the discounted dividend model must be used to value the stock. One common technique is to assume that the Miller-Modigliani hypothesis of dividend irrelevance is true, and therefore replace the stocks's dividend D with E earnings per share.
But this has the effect of double counting the earnings. The model's equation recognizes the trade off between paying dividends and the growth realized by reinvested earnings. It incorporates both factors. By replacing the (lack of) dividend with earnings, and multiplying by the growth from those earnings, you double count.
c) The stock price resulting from the Gordon model is hyper-sensitive to the growth rate  chosen.
chosen.
References
- ^ Investopedia – Digging Into The Dividend Discount Model
- ^ Gordon, Myron J. (1959). "Dividends, Earnings and Stock Prices". Review of Economics and Statistics (The MIT Press) 41 (2): 99–105. doi:10.2307/1927792. JSTOR 1927792.
- ^ Spreadsheet for variable inputs to Gordon Model
Further reading
- Gordon, Myron J. (1962). The Investment, Financing, and Valuation of the Corporation. Homewood, IL: R. D. Irwin.
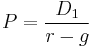
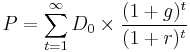
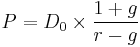
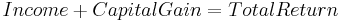
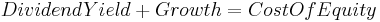
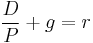
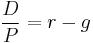
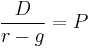
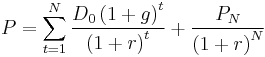
![P = \frac{D_0 \left( 1 %2B g \right)}{r-g} \left[ 1- \frac{\left( 1%2Bg \right)^N}{\left( 1 %2B r \right)^N} \right]
%2B \frac{D_0 \left( 1 %2B g \right)^N \left( 1 %2B g_\infty \right)}{\left( 1 %2B r \right)^N \left( r - g_\infty \right)},](/2012-wikipedia_en_all_nopic_01_2012/I/f1cb8ebac361b8aa3df41c2da4efae5e.png)